Field Theory - Online Tutorial 1 - New

by Kevin Tang , new update May 26, 2014

[main pages]

 

Q1 -

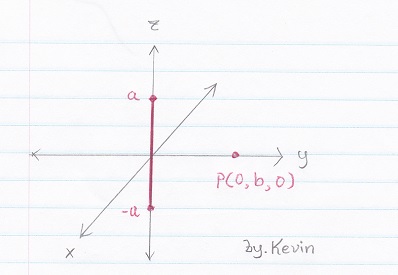
A charge ρl [C/m] is uniformly distributed on the line −a < z < a.   and point P given P (0, b, 0)

Find the following...

 

* Please review this question, as I didn't solve it fully today ~ good luck :)

* Notice: any BOLD letter means that variable is a VECTOR.

 

1a) Draw the diagram

1b) Find r, r', r − r', | r − r' | and dQ.

1c) E at point (0, b, 0)

 

1a) Draw the diagram..

 

Solving Time: 3 min

 

SOLUTION 1a)

Shown in Figure #1 below...

 

                                Figure # 1

 

 

1b) Find r, r', r − r', | r − r' | and dQ.

 

Solving Time : 5 min

 

 

Let's have fun and give a try...(click the answer that you think it is correct)

 

Which one is r?

 
A
  • r = b
  • Wrong Answer
 B
  • r = aax + 0ay + 0az
  • Wrong Answer
 C
  • r = 0ax + bay + 0az
  • Correct!
D
  • r = baρ
  • Wrong Answer

 

 

 

Which one is r'?

A

  • r' = 0ax + 0ay + aaz
  • Wrong Answer

 

B

  • r' = 0ax + bay + z'az
  • Correct!

 

C

  • r' = 0ax + bay + aaz
  • Wrong Answer

 

 

 

Than you can get can get r − r' and | r − r' |

 

Next, which one is dQ?

 

A

  • dQ = ρl az dz'
  • Wrong Answer

 

B

  • dQ = ρl z' dz'
  • Wrong Answer

 

C

  • dQ = ρl dz'
  • Correct!

 

 

 

SOLUTION 1b)

Answer for r, r', r − r', | r − r' | and dQ.

Detail solution shown as following (shown in Figure #2)...

 

                                Figure # 2

 

1c) E at point (0, b, 0)

 

 

Solving Time : 15 min

 

 

SOLUTION 1c)

 

Actually the solution is much longer than I expected, please take a good look...

 

First, sub everything into dE

 

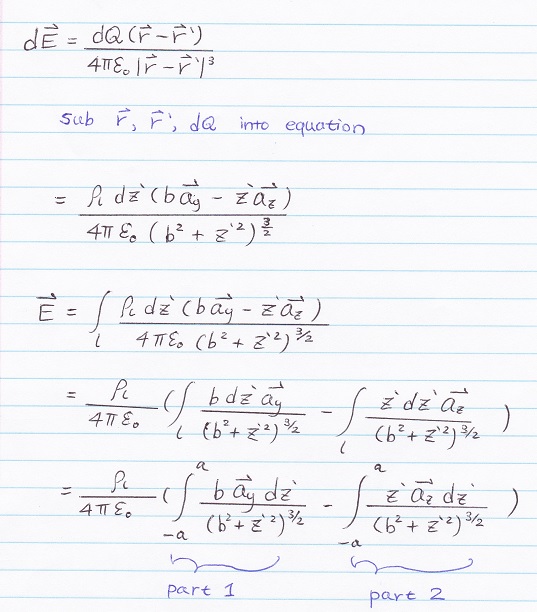
                                Figure # 3

 

Second, split the integral into 2 PART.

 

Remember, as I said in class, you can visually see that az part (part 2) will cancel out to zero due to symmetric,

however, here I am still going to show you how its lead to zero.

 

 

Now, we start with ay part (part 1) of the integral...(shown in Figure #4)

you need to applied integral by trigonometric substitution (or you can directly check it on Integral Table)

 

                                Figure # 4

 

 

.

.

.

.

Part 2, az part of integral, its will cancel out and lead to zero as shown following (shown in Figure #5)...

 

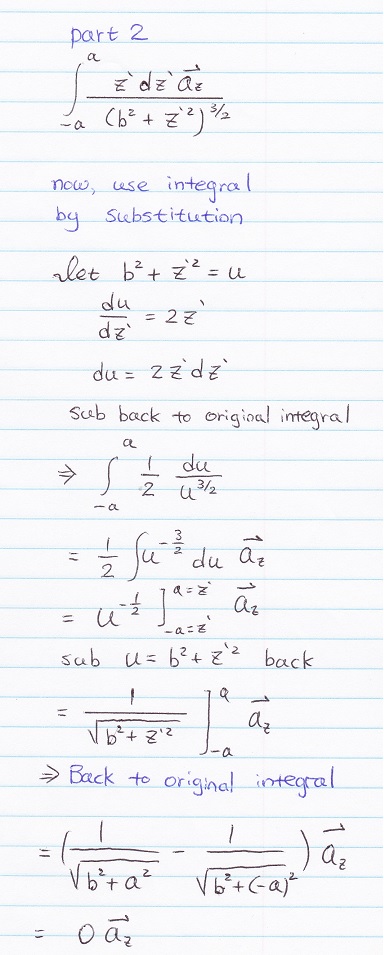
                                Figure # 5

 

Last step, sub everything into E, and you will get the final answer (shown in Figure #6) :)

 

                                Figure # 6

 

 

[back to top]

 

 

 

 

 

You may leave me any message if you have any questions, I will try to answer ASAP, thanks and good luck :)